FÍSICA ACÚSTICA PARA LEIGOS I – O TIMBRE. Iniciamos aqui uma nova fase da série Home Studio, procurando conhecer as bases teóricas e aplicá-las imediatamente, para seu melhor assentamento prático.
A música tem quatro propriedades: Altura, Duração, Intensidade e Timbre. Esta última tem sido exaustivamente usada na produção musical, muitas vezes sem embasamento teórico. Com o estudo do Timbre vamos conhecer melhor as diferenças entre instrumentos musicais reais e virtuais, e até mesmo instrumentos inexistentes na vida real. Muitos aspirantes a produtores passam batido por uma série de estudos fundamentais, abrindo suas DAWs e metendo o dedo em suas possibilidades, até que, a um dado momento, percebem que sua curva de aprendizado poderia ser reduzida, ao mesmo tempo em que resultados mais personalizados poderiam ser alcançados. Antes, porém, será necessário uma introdução teórica à Acústica, que nos dará uma idéia final do que é o som, para diferenciarmos os sopros, os sons eletroacústicos, a percussão, as cordas e todas as variações da propriedade do som chamada Timbre.
A evolução da ciência nos proporcionou condições de “ver” cada forma de som, através da observação da forma de sua “onda” sonora, obtida através de aparelhos específicos. Aí torna-se bem claro o conceito de timbre, e mesmo outros como os das outras propriedades do som. Vamos abordar o timbre de forma ainda inédita em cursos semelhantes, que têm se revelado carentes de informações técnicas e evidentemente também as científicas, destas, de maneira especial as mais recentes. Estudaremos generalizadamente o timbre, as bases científicas do som e de sua criação. É grande a quantidade de instrumentistas que se pode observar completamente dominados por uma parafernália eletrônica, sem usar essa mesma aparelhagem de forma criativa ou mesmo interessante. E isso deve-se ao desconhecimento de uma forma de onda, ou de fase, por exemplo, nada difíceis de aprender, tendo sido considerados os conhecimentos eletroacústicos secundários num mundo cada vez mais tecnológico.
A tecnologia não substitui a criação, mas eleva-a a um outro estágio de observação, igualmente criativo, numa soma ideal. Trabalhar com tais elementos sem conhecimentos específicos é perda de tempo, no mínimo. Procuramos reunir informações úteis a quem toca um instrumento e lida com sofisticações no seu uso, desde um simples captador, até uma guitarra com pedais diversos. Para melhor entendê-las é necessário re-observar conceitos como os do som, da música, do barulho e do vento. Começaremos e terminaremos com linguagem simples, sem usar termos muito desconhecidos, para que o desconhecido se torne conhecido claramente.
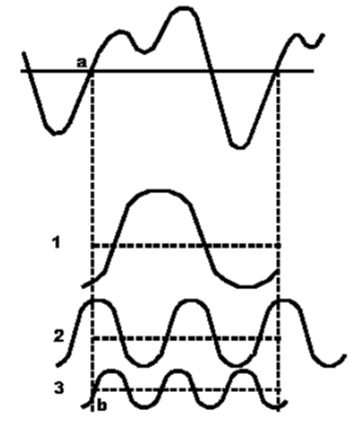
Vamos partir de uma atividade musical simples, como por exemplo, o som de um violão solando uma melodia fácil, nem muito agudo, nem muito grave. Vejamos se podemos descobrir o que ocorre com o ar que está entre o violão e o ouvido de alguém que esteja escutando. É nesse ar que acontece um fenômeno que, à primeira vista poderíamos chamar de “onda” sonora, à semelhança das ondas do mar, que acontecem num meio líquido. Mais preciso do que o termo “onda” será o termo “pulsação”, que se adequada melhor ao fenômeno que não é único, isolado, mas serial, consecutivo. Compreenderemos melhor a noção de “pulsação” se examinarmos o batimento do pulso em nossa munheca. Ao princípio de cada uma das pulsações a pressão do sangue contra a parede da veia é muito leve. Essa pressão aumenta até o ponto culminante, onde há a maior pressão, e passa a diminuir para chegar à mesma condição de baixa pressão com que havia começado a pulsação. As diferentes pressões contra a parede da veia se devem à variação na densidade do sangue durante a pulsação, pela ação bombeadora do coração. Esta variação é rápida, mas as suaves paredes da veia oferecem pouca resistência à pressão, de forma que podemos sentir o batimento com os dedos. Podemos traçar um gráfico (uma linha) representando as variadas pressões do sangue contra o dedo durante várias pulsações, que teria o seguinte aspecto:
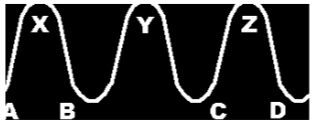
Nos pontos A, B e C começam as pulsações; e nos X, Y e Z atinge-se os pontos culminantes, de maior pressão. A primeira pulsação vai do ponto A até o B, a segunda do ponto B até o C, e assim por diante. O gráfico representa não só as diferentes pressões contra as paredes da veia, como também as variações da densidade do sangue, que causam as pressões.
Compare agora o primeiro gráfico, uma hipótese, com um segundo gráfico feito por um aparelho especial para medir o pulso:
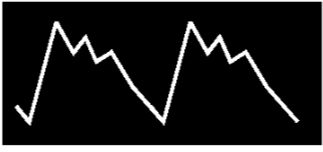
De início notamos muitas irregularidades, devido às rápidas variações da densidade do sangue durante as pulsações. Do mesmo modo que o gráfico 1, o segundo mostra pontos de pressão baixa ao começo de cada pulsação, e de alta pressão nos momentos culminantes. A diferença básica está nos momentos em que, tendo ocorrido um ponto culminante, a pressão diminui desuniformemente, aos pulinhos, formando uma linha descendente irregular. É a variação da densidade do sangue sendo representada mais fielmente, medida cuidadosamente.
O professor Dayton C. Miller, da Case School of Applied Science, nos EUA, construiu um aparelho destinado a dar a forma gráfica aos sons captados na atmosfera “musicalmente ativa”. Este aparelho – o Fonodeik – traça o gráfico das variações da densidade atmosférica causadas pelas pulsações sonoras, da mesma maneira que o aparelho medidor da pulsação sanguínea traça o das variações da densidade do sangue, produzidas pelo coração. Agora já podemos entender o que há entre o violão e o ouvido do ouvinte. É o que se passa no gráfico 3.
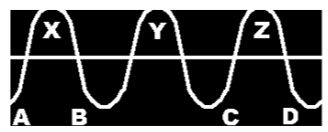
Lembrando que o gráfico mostra a densidade variável do ar durante várias pulsações, veremos que a densidade é menor nos pontos A, B e C, onde começam as pulsações e que a densidade aumenta até alcançar os pontos culminantes X, Y e Z, decrescendo logo para os finais em B, C e D respectivamente. A primeira pulsação vai de A até B, a segunda de B até C e assim por diante. Desde o princípio da pulsação até o ponto culminante o aumento da densidade é constante, e desde o ponto culminante até o final decresce constantemente. A linha horizontal é um “nível de equilíbrio” imaginário.
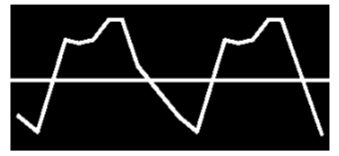
O gráfico 4 é um pouco mais irregular do que o do violão. É de uma nota MI ao violino. Entre o princípio da pulsação e o ponto culminante o aumento da densidade não é sempre constante; há um breve período durante o qual a densidade não só não mostra aumento algum, senão decresce um pouco. Mas desde o ponto culminante até o fim decresce constantemente. O gráfico de uma voz de mulher (soprano) apresenta o inverso da situação anterior. Desde o princípio da pulsação até o ponto culminante a densidade aumenta continuadamente, mas desde o ponto culminante até o final há um período durante o qual a densidade não só decresce como mostra um aumento grande. O gráfico é o 5:
O gráfico 6 é de um clarinete na região aguda, muito irregular. Desde o começo até o ponto culminante a densidade sempre vai aumentando, mas entre o ponto culminante e o final há quatro períodos de aumento, dois pequenos e dois grandes:
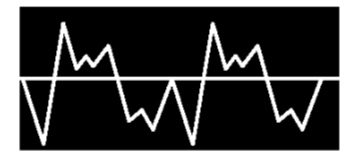
O gráfico 7 é da voz masculina (um barítono), como cinco “cristas” entre o começo da pulsação e o ponto culminante, mas nenhuma entre o ponto culminante e o final:
Praticamente as mesmas condições persistem no gráfico do som de trompa (gráfico 8). Há cinco cristas entre o princípio da pulsação e o ponto culminante, mas nenhuma entre este e o final. De fato, o som da trompa se assemelha ao da voz de barítono.
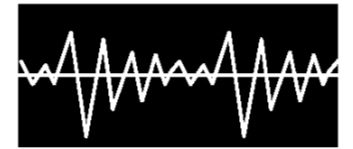
Já o som do oboé mostra duas cristas entre o começo da pulsação e o ponto culminante, e três entre o ponto culminante e o final, conforme mostra o gráfico 9.
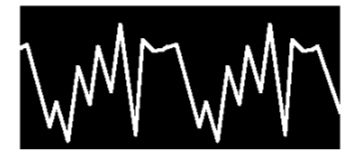
O gráfico da voz de um cantor baixo mostra cinco cristas entre o começo e o ponto culminante, e nenhuma deste até o final, chegando a parecer com o da voz do barítono e da trompa, como se vê a seguir:
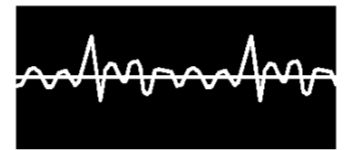
O gráfico (no 11) do som de um clarinete em região grave mostra pelo menos oito cristas entre o princípio da pulsação e o ponto culminante, e uma entre o ponto culminante e o final.
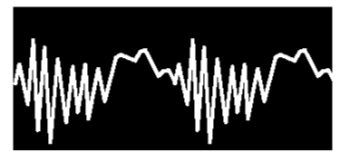
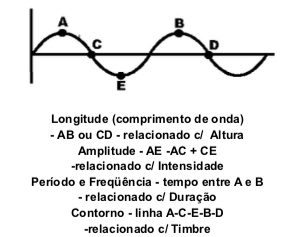
O gráfico do som de uma campainha (12) é tão irregular que é impossível descobrir um princípio, um ponto culminante ou final para qualquer período do qual se possa dizer que constitui uma pulsação. O som carece de um “período pulsatório” definido, não sendo periódico. Todos os demais gráficos até aqui apresentados são “periódicos”, isto é, o som divide-se em períodos durante os quais o gráfico de algum período é a duplicação do gráfico de algum outro período. Após observarmos alguns gráficos de instrumentos de timbres os mais diversos, pudemos concluir que os vários gráficos diferem em três aspectos: a Longitude da pulsação, a Amplitude da pulsação e o seu Contorno.
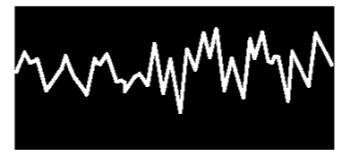
Se tomarmos o gráfico 13 para ilustrar, e traçarmos uma linha que passa pelos pontos X, Y e Z (pontos culminantes), e outra linha que passa pelos pontos A, B e C (inícios de pulsação), chamamos a distância de X e Y de Longitude, a distância de A e X de amplitude, e o traçado do gráfico, do princípio de uma pulsação ao começo da próxima de Contorno. Podemos examinar vários gráficos de uma nota Lá, produzidos por diferentes instrumentos que soam em distintos graus de intensidade que veremos as pulsações variarem de amplitude e de contorno, porém, com a mesma longitude. Disso podemos deduzir que as pulsações de sons de mesma Altura têm a mesma longitude. Se examinarmos os gráficos de sons mais agudos, veremos que as pulsações são mais curtas, e os gráficos de sons mais graves resultam em pulsações mais largas. A Altura, então, depende da Longitude de uma pulsação.
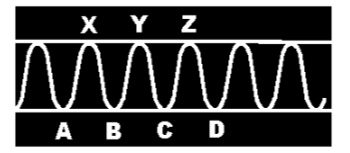
Passamos a observar agora o gráfico (14) de uma nota de qualquer instrumento fazendo um “diminuindo – crescendo”. Todas as pulsações são de mesma Longitude, mas se fazem cada vez mais estreitas durante o “diminuindo”, e cada vez mais largas durante o “crescendo”. Chegamos à conclusão, pois, de que a Intensidade de um som depende da Amplitude de seu gráfico ou, em outras palavras, da variação de densidade da pulsação. Observe o gráfico:
Aparentemente, instrumentos diferentes dão diferentes Contornos para as notas de mesma Altura. E, já que as notas de mesma Altura e Intensidade só diferem em qualidade, chegamos à conclusão de que a qualidade do som, ou TIMBRE, depende do Contorno do gráfico do som, ou seja, da velocidade em que muda a densidade da pulsação. A Altura é, então, a “forma sensorial” em que se manifesta a Longitude de uma pulsação periódica. A Intensidade é a forma sensorial em que apresenta a variação de densidade, e o Timbre é a forma sensorial com que se apresenta a velocidade de mudança da densidade na pulsação.
Por que é, então, que se produzem irregularidades nos contornos de alguns dos gráficos já observados? O mais regular de todos os gráficos é o que se consegue com o som de um diapasão normal (gráfico 15).
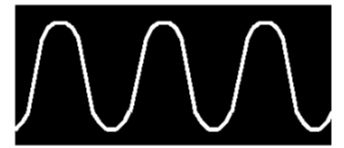
A evidência matemática, pouco complicada para ser detalhada aqui, mostra que o som de um diapasão normal é o mais simples dos sons musicais. Entretanto, difere pouco do violão (gráfico 3). O som do violino (gráfico 5) é radicalmente diferente. Mas, se fizermos soar juntos três diapasões normais, como o primeiro diapasão tem uma pulsação de igual longitude do que a do som do violino, o segundo, uma pulsação de metade dessa longitude e o terceiro uma pulsação de um terço da mesma longitude, e os três têm, portanto, forças relativas de 165, 60 e 27, respectivamente, ouviremos um som cuja qualidade apenas se distingue da do som do violino já mostrado, e cujo gráfico (16), é quase idêntico ao gráfico 4 (violino). Veja e entenda:
O número de parciais presentes em um som depende de três coisas: o instrumento que o produz, a posição do som na extensão (tessitura) do instrumento e da intensidade do som. Quanto mais alto está situado o som na extensão do instrumento menor será o número de seus parciais. O som de violino (gráfico 4) analisado há pouco tinha parciais muito débeis, acima do terceiro (da ordem em que se sucedem os parciais, 1; 1/2; 1/3, etc.). A nota usada foi SI.
Se tivesse sido usada uma nota mais ou menos uma oitava mais baixa, teria mostrado muito mais parciais. A mesma regra pode ser aplicada aos demais instrumentos de corda. O que possui o registro mais grave terá o maior número de parciais. O som da flauta é rico em parciais na região inferior, e acima da primeira oitava os parciais são muito fracos, com exceção do primeiro. O clarinete é rico em parciais na parte grave de sua extensão, tendo poucos na parte média, mas não tão fracos quanto os da flauta. O oboé e o fagote são extremamente ricos em toda sua extensão, também acentuadamente na região grave. A trompa mostra, às vezes, trinta parciais nas notas graves, ainda que nem tanto nas mais altas. Os outros metais são também ricos em parciais, principalmente os trumpetes e trombones. O número de parciais de uma nota depende também da intensidade com que é tocada, já que um aumento de intensidade provoca um aumento do seu número. É possível, no entanto, que o número de parciais esteja presente em uma nota piano e em uma forte (p e f), mas os parciais mais altos da nota piano estejam abaixo do nível de audição. Além dos sons chamados parciais, presentes em quase todos os sons produzidos pelos instrumentos musicais, encontram-se contidos no conjunto sonoro outros sons conhecidos pelo nome de diferenciais. Estes resultam da combinação dos parciais. Cada dois sons parciais produzem um diferencial cuja altura é mais grave do que a do parcial mais agudo. Mas, ainda com relação aos parciais e ao som composto que formam, vamos observar duas coisas:
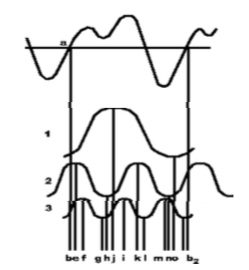
Primeiro: os parciais não se apresentam ao ouvido como três pulsações diferentes, 1, 2 e 3, mas se unem para formar uma pulsação, que é um COMPOSTO das 3. Segundo: os parciais às vezes atuam juntos, para aumentar ou diminuir a intensidade, mas frequentemente atuam em oposição, pois alguns deles tendem a aumentar a intensidade e outros a diminuí-la. Dos doze períodos mostrados no gráfico, nos instantes b, e, f, g, h, i, j, k, l, m, n, o, p & b2 (este último repetição do primeiro b) há somente 4 períodos durante os quais os três parciais atuam em conjunto: durante o período de h até i, e durante o período que começa em p, passando de b até e, existe um só período contínuo, todos os parciais aumentam a densidade. Durante o período de k até l, e durante o período de m até n, os parciais atuam em conjunto para diminuir a densidade. Durante os outros oito períodos os parciais atuam em oposição, alguns aumentando a densidade, outros diminuindo-a. E o mesmo acontece se o número de parciais que compõe um som é maior ou menor que três, ou se o número total de parciais que atua sobre uma partícula de ar procedem todos do mesmo instrumento, ou de uma centena deles. Temos então forças que se alinham impulsionando a partícula em certa direção, e outras forças opostas atuando em conjunto para outra direção. A partícula varia em função da força relativa das direções a tomar. Não importa se todos os parciais vêm de um só instrumento ou de muitos, se eles tocam em uníssono ou em completa harmonia: é uma só pulsação composta que vai ao ouvido em dado momento, e não varia.
Parece então que no solo tocado pelo violão que deu início ao nosso estudo e nosso ouvido há milhares de pulsações, vinculadas umas com as outras de tal maneira que se unem em uma só pulsação composta. As verdadeiras longitudes e amplitudes das pulsações são diferentes do que se mostra nos gráficos. A verdadeira longitude da pulsação atmosférica para o Lá do violino é mais ou menos de 75 cm. A do violoncelo, uma oitava mais baixa, em torno de 1,50 cm, e a do contrabaixo, três oitavas abaixo da do violino, mais ou menos de 6 m. A da corda mais grave do contrabaixo tem aproximadamente 8 m. A verdadeira longitude da pulsação atmosférica de Lá uma oitava mais alta que a do violino está em torno de 40 cm, e o Lá duas oitavas acima do Lá inicial tem longitude aproximada de 20 cm. A pulsação atmosférica de qualquer som é duas vezes mais larga do que a de sua oitava superior. Porém, nos gráficos, as pulsações se apresentam para maior conveniência visual, com uma longitude uniforme compreendida entre uns 2 e 5 cm., sem reparar nas verdadeiras longitudes atmosféricas. Da mesma maneira que a longitude das pulsações nos gráficos é muito menor que na atmosfera, a amplitude das pulsações se apresenta nos gráficos muito maior que as verdadeiras pulsações. Os sons musicais de maior intensidade movem uma partícula de ar somente 25 décimos de milésimos de centímetro, e um som é apenas audível às vezes só a nove e meio bilionésimos de centímetro. Portanto, a amplitude de verdadeira pulsação produzida por música provavelmente nunca será superior a 25 décimos de milésimo de cm, e, usualmente, não maior do que 25 milionésimos de cm. A verdadeira longitude das pulsações na atmosfera variam entre 24 metros, nos casos mais graves, até 1,25 cm, nos casos mais agudos. A verdadeira amplitude dessas pulsações varia de 25 décimos de milésimo de cm, até um valor que quase não é mensurável.
Se acrescentarmos outros diapasões ao grupo, com pulsações de 1/4, 1/5, 1/6, 1/7 etc., da longitude de pulsação do violino, o som composto que se ouviria e seu gráfico se aproximariam ainda mais do gráfico do violino. Evidentemente então, esse som de violino se compõe de vários sons simples cujas longitudes estão em relação com o som do violino em proporções de 1, 1/2, 1/3, 1/4, 1/5, etc… Os sons destes diversos diapasões normais chamam-se PARCIAIS do som composto que se ouve quando soam todos a um mesmo tempo, ou quando soa o do violino. Os números 165, 60, 27 e outros não determinados são as forças relativas do som do violino, representam a intensidade dos diferentes parciais, e podemos chamá-los de coeficientes dos parciais. Os coeficientes dos dez primeiros parciais do som da voz masculina de barítono (gráfico no 7) são, respectivamente 4, 15, 18, 12, 20, 60, 21, 16, 2 e 3. Isto significa que o mais forte parcial do som é o 6o (60), e seguem-se em ordem decrescente, o 7o, 5o, 3o, o 8o, o 2o, o 4o, o 1o, o 10 o e 9o. Os coeficientes dos doze primeiros parciais do som de clarinete (gráfico no 11) são 29, 7, 20, 1, 2, 6, 6, 8, 16, 9, 30 e 35. O parcial mais potente é o 12o (35), e depois dele o 11o, o 1o, o 3o, o 9o, o 10o, o 8o, o 2o, o 6o e o 7o (iguais), o 5o e o 4o. Determinar os coeficientes dos parciais de um som musical dá muito trabalho, necessitando-se fazer difíceis cálculos matemáticos. Atualmente esses cálculos são feitos por uma máquina chamada Analisador Harmônico. Um analisador similar, porém muito mais complicado, é usado pela Inspeção de Costas e Geodésica dos EUA, para calcular a altura das marés. A exatidão dos resultados alcançados por esse método são comprovados pela sua utilização, com vários anos de antecipação, pela navegação marítima para conhecer quais as condições de um porto em qualquer momento futuro em qualquer parte do mundo. Isso em se tratando de sons audíveis pelo ouvido humano. A pulsação do som da voz do barítono (gráfico no 7) terá como longitude de seu primeiro parcial um pouco mais de 2 m. Os parciais restantes terão longitudes que encontraremos dividindo 2 m pelo número de cada um deles. E essa pulsação dentro de pulsações terá diferentes amplitudes que dependerão dos coeficientes dos diferentes parciais, sem nenhuma delas exceder os 25 décimos de milésimo de cm. E também não se pode perder de vista que os gráficos representam as variações de densidade do ar na atmosfera ao largo de toda a longitude da pulsação. Observe o seguinte gráfico:
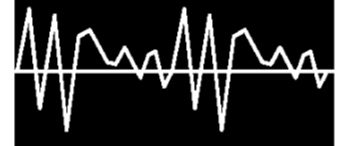
A pulsação total mede um pouco mais de 2 metros. As regiões de mínima densidade se farão a intervalos de 1/6 dos 2 m, ou seja, uns 35 cm, desde o começo da pulsação, e as zonas de máxima densidade ficarão na metade do caminho entre as de mínima densidade e as distâncias aproximadas de 18 cm, 53 cm, 89 cm, 124 cm, 160 cm e 195 cm, desde o princípio da pulsação até a variação da densidade da atmosfera durante toda a pulsação. Se assemelharia com o gráfico a seguir, que apresenta as mudanças da densidade atmosférica ao largo de mais ou menos 6 metros, quase três pulsações completas de 2 m encontrando-se cada uma delas justamente no mesmo ponto, as zonas de máxima densidade, marcadas respectivamente em 0 m, 2 m e 6 metros.
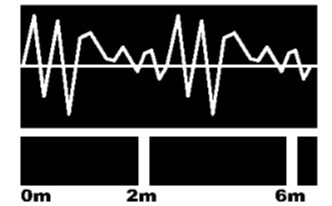
Mesmo assim, o gráfico está grosseiramente exagerado, a verdadeira variação é muito pequena, e representa adições e subtrações de densidade muito menores que as de nosso vazio mais perfeito. As partículas de ar se movem de suas posições distanciais infinitesimais, microscópicas e sutis. Podemos agora dar uma definição aproximada do que é o som: É a sucessão de pulsações atmosféricas capazes de produzir a sensação auditiva. Se as pulsações são muito lentas, rápidas, fracas ou fortes para que possam ser captadas pelo ouvido, então não chegaremos a chamá-las de som. Mas se o ouvido é capaz de apreciá-las, então vamos chamá-las de som, às sensações que produzem de audição. Para que o som seja musical, as pulsações devem ser periódicas. Logo, o SOM MUSICAL é uma sucessão de pulsações atmosféricas periódicas capazes de serem ouvidas. Conhecemos agora o que são, na realidade, os sons musicais. Mas não podemos considerá-los e à música como sendo a mesma coisa. Os sons musicais devem ser trabalhados nos seus parâmetros Altura, Duração, Intensidade e Timbre para que se tornem música. Como conclusão do estudo das pulsações sonoras, temos a observação de cada propriedade do som e seu relacionamento com o respectivo gráfico de variação da densidade do ar. Desses relacionamentos podemos extrair mais um gráfico demonstrativo:
Acabamos de ver que o Timbre nada mais é do que a qualidade do som produzido, sua caracterização, sua particularidade. Logicamente existem tantos timbres quanto são os instrumentos existentes. Em muitos instrumentos, a notação da pauta é a mesma do som real produzido, mas há também instrumentos em que o som é uma coisa e a notação outra. Os instrumentos de sopro têm, devido à maneira como foram construídos, suas próprias escalas. Quando essas são da tonalidade de Dó Maior, o som coincide com a notação. Mas no caso de um instrumento que tenha Lá maior como escala, a escala de Dó maior soará como se fosse Lá maior. Se quisermos produzir o som da escala de Dó maior é necessário tocar usando a escala de Mi bemol maior. O instrumento, estando em Lá maior, precisa ser TRANSPOSTO uma terça menor abaixo. Logo, é preciso tocar uma terça menor acima do que se deseja. Vejamos um exemplo: um clarinete em Si bemol (construído usando a escala de Si bemol maior) toca uma nota que se escreve como DÓ. O som ouvido será uma nota SI BEMOL. Logo, se você quiser ouvir a nota DÓ de fato, terá que escrever a nota RÉ, um tom acima, ou uma SEGUNDA MAIOR acima.
Chegamos aqui a um assunto que envolve a ESCRITA MUSICAL, que será assunto de nossa próxima seção. O conhecimento de FÍSICA ACÚSTICA associado à notação musical é o melhor dos mundos para o pleno conhecimento – com consciência – do que acontece no mundo da produção musical. Claro, temos aqueles que desenvolveram algum tipo de pavor ou ligeira fobia por assuntos como Física Acústica ou Notação Musical. Estes poderiam se sentir melhor se lembrarem que desde a Grécia Antiga as 4 matérias mais importantes eram a Astronomia, a Geometria, a Matemática (Aritmética) e a Música, o chamado Quadrivium. A música não é apenas entretenimento, envolve muitas outras aplicações, mas infelizmente uma educação deficiente nos é hoje oferecida, e precisamos buscar tapar seus buracos.
